Cours de physique-chimie 2nde, chapitre 11:Interactions et forces

I Les interactions

I.1) Définition

Si un système appelé « A » agit sur un autre système appelé « B » alors le système B agit aussi simultanément sur le système A

Toute action d’un système A sur un système B s’accompagne d’une action du système B sur le système A, ce couple d’actions est appelé « interaction ».

Quelle que soit la situation (pour tous les systèmes en mouvement ou immobiles) toute action fait partie d’une interaction.

I.2) Le diagramme « système – interaction »

Un diagramme système-interaction est un un schéma qui indique :

Le système étudié (on note son nom au centre, on l’entoure et on le distingue des autres systèmes en soulignant, ou en utilisant une autre couleur)
Les systèmes qui interagissent avec le système étudié (leurs noms sont indiqués autour de celui du système étudié)
Les interactions de contact sont représentées par une double flèche pleine
Les interactions à distance qui sont représentées par une double flèche en pointillés.

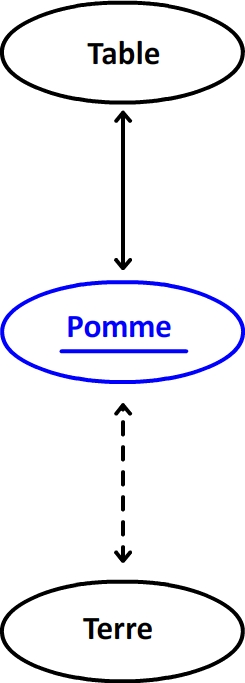
Exemple de diagramme Système interaction: Une pomme immobile posée sur une table.

Le système que l’on décide d’étudier est la pomme, elle interagit avec la table (avec laquelle elle est en contact) et la Terre (son poids correspond à une interaction gravitationnelle avec la Terre).

Important

Une interaction est une interaction de contact si elle ne peut s’exercer qu’à condition que les deux systèmes en interaction soient en contact.

Une interaction est une interaction à distance si elle peut s’exercer même sans contact entre les systèmes qui interagissent ( les interactions gravitationnelles, électrostatiques et magnétiques sont toujours des interactions à distance)

II Modélisation d’une action par une force

Quand un système A et un système B interagissent alors l’action du système A sur le système B peut être modélisée par une « force ».

Cette force se note « [latex size=1 color=000000 background=d3e4ec ]\displaystyle {F_{A/B}} [/latex]» avec « F » comme « Force », on note en indice tout d’abord « A » (l’auteur de l’action) puis une barre « / » suivie de « B » ( le système qui subit l’action).

Cette force est caractérisée par :

son point d’application (le point du système B où le système A agit)
sa direction (verticale, horizontale, oblique…)
son sens (vers la gauche, vers la droite, vers le bas, vers le haut….)
sa valeur exprimée en Newton (symbole N)

Cette force peut être représentée par un vecteur force noté ^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{A/B}} [/latex]} dont :

l’origine correspond au point d’application
la direction est la même que celui de la force
le sens est le même que celui de la force
la norme (la longueur) est proportionnelle à la valeur de la force.

III Principe des actions réciproques

Si un système « A » agit sur un système « B » alors il y a interaction entre les deux systèmes et le système « B » agit également sur le système « A ».

S’il y a interaction entre un système A et un système B il y a donc :

Une force ^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{A/B}} [/latex]} qu’exerce « A » sur « B »
Une force ^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{B/A}} [/latex]} qu’exerce « B » sur « A »

D’après le principe des actions réciproques ces deux forces ont :

la même direction
la même valeur
des sens opposés

Le principe des actions réciproques peut se traduire par la relation suivante :

^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{A/B}} [/latex]} = – ^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{B/A}} [/latex]}

Par exemple, si un système « A » exerce sur un système « B » une force ^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{A/B}} [/latex]}:

horizontale
de valeur 25 N
orientée vers la droite

Alors, d’après le principe des actions réciproques , la force exercée par le système « B » sur le système « A » est une force :

qui est aussi horizontale
a aussi une valeur de 25 N
a un sens opposé et par conséquent est orientée vers la gauche.

IV Quelques exemples de forces de contact

IV.1) objet suspendu à un fil

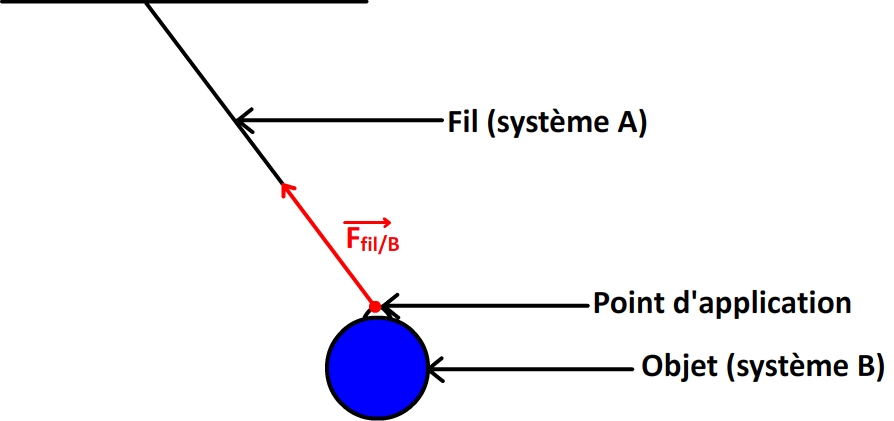
Si un objet (système B) est suspendu à un fil (système A) alors le fil exerce une force ^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{Fil/B}} [/latex]} dont les caractéristiques sont les suivantes :

Le point d’application est le point où le fil est attaché à l’objet
La direction est la même que celle du fil
Le fil soutient l’objet, la force est donc orientée de l’objet vers le fil

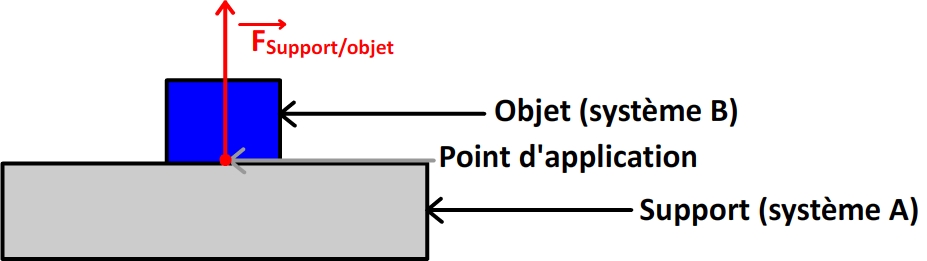
IV.2) Un objet immobile posé sur un support

Un objet immobile (Système « B») est posé sur un support (système « A »), il n’est soumis qu’à son propre poids et à la force de contact exercée par le support.

Le support exerce une force ^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{support/objet}} [/latex]} qui a les caractéristiques suivantes :

Le point d’application est le centre de la surface de contact entre le support et l’objet
La direction est verticale
La force est orientée vers le haut (s’oppose au poids)
La valeur est la même que celle du poids

V Loi de l’interaction gravitationnelle

V.1) L’interaction gravitationnelle

Définition

Du seul fait qu’ils possèdent une masse deux systèmes interagissent, ils exercent entre eux une interaction dite gravitationnelle.

Si un système « A » possède une m_A et système B possède une masse m_B alors il existe une interaction gravitationnelle entre ces deux systèmes.

V.2) Caractéristiques de la force de gravitation

Un système « A » de masse m_A situé en point A de l’espace exerce une force gravitationnelle ^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{A/B}} [/latex]} sur un système B de masse m_B situé en point B de l’espace et la distance AB entre les points A et B est notée « d »:

La force de gravitation ^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{A/B}} [/latex]} s’applique au point B
a même direction que la droite (AB)
La force est attractive (orientée de B vers A)
sa valeur est donnée par loi de gravitation :

[latex size=1 color=000000 background=d3e4ec]\displaystyle F_{A/B} = G \times \frac{m_{A} \times m_{B}}{d^{2}}[/latex]

où :

G est la constante de gravitation universelle, G = 6,67×10^–11 N·m²·kg^-2 ( 6,67×10^–11 S.I.)
La masse m_A du système A et la masse m_B du système B sont exprimées en kilogramme (kg)
La distance « d » entre les deux systèmes est exprimée en mètre (m)
La force est en Newton (N)

D’après le principe des actions réciproques la force de gravitation ^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{B/A}} [/latex]} exercée par le système « B » sur le système « A » a donc les caractéristiques suivantes :

s’applique au point A
a même direction que la droite (AB)
est orientée de A vers B
a aussi comme valeur [latex size=1 color=000000 background=d3e4ec]\displaystyle F_{A/B} = G \times \frac{m_{A} \times m_{B}}{d^{2}}[/latex]

V.3 Poids et force de gravitation

Définition

Lorsqu’un système « A » est à la surface (ou proche de la surface) d’une planète alors le poids de ce système (noté P_A) peut être assimilé à la force de gravitation ^{[latex size=1 color=000000 background=d3e4ec ] \displaystyle \overrightarrow{F_{Planete/A}} [/latex]} exercée par la planète sur le système A :

^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{P_{A}} [/latex]} = ^{[latex size=1 color=000000 background=d3e4ec ]\displaystyle \overrightarrow{F_{Planete/A}} [/latex]}

[latex size=1 color=000000 background=d3e4ec ]\displaystyle {P_{A}} [/latex] = [latex size=1 color=000000 background=d3e4ec]\displaystyle G \times \frac{m_{A} \times m_{planete}}{d^{2}}[/latex]

Par définition le système A se trouve à la surface de la planète par conséquent la distance qui les sépare correspond au rayon de la planète R_planète

L’expression du poids devient donc :

[latex size=1 color=000000 background=d3e4ec ]\displaystyle {P_{A}} [/latex] = [latex size=1 color=000000 background=d3e4ec]\displaystyle G \times \frac{m_{A} \times m_{planete}}{{R_{planete}}^{2}}[/latex]

[latex size=1 color=000000 background=d3e4ec ]\displaystyle {P_{A}} [/latex] = [latex size=1 color=000000 background=d3e4ec]\displaystyle \frac{G \times m_{planete}}{{R_{planete}}^{2}} \times m_{A}[/latex]

Le facteur de proportionnalité [latex size=1 color=000000 background=d3e4ec]\displaystyle \frac{G \times m_{planete}}{{R_{planete}}^{2}} [/latex] qui apparaît dans cette expression peut être noté « g » , il ne dépend pas du système « A » considéré mais uniquement des caractéristiques de la planète (son rayon et sa masse).

On retrouve l’expression qui permet de calculer la valeur du poids (vue au collège) :

P = m x g

g est appelé intensité de la pesanteur ou champ de pesanteur, il s’exprime en Newton par kilogramme (N.kg^-1) et peut être déterminé grâce à la relation suivante :

[latex size=1 color=000000 background=d3e4ec]\displaystyle g = \frac{G \times m_{planete}}{{R_{planete}}^{2}} [/latex]

Dans le cas de la planète Terre g = 9,8 N.kg^-1.

Le cours commenté est disponible en vidéo: